Es decir,
Representación
Sea R una relación antisimétrica aplicada sobre un conjunto A, entonces R tiene una representación particular para cada forma de describir una relación binaria.- Como pares ordenados,
- Como matriz de adyacencia M, la matriz
no tiene ningún 2 salvo, a lo sumo, en la diagonal.
- Como grafo, éste no contendrá ciclos, pero sí podrá tener bucles en sus nodos.
Sea A un conjunto cualquiera:
R es antisimétrica≡
∀ x ∀ y (xRy & yRx ⇒ y=x)
- Sea
, 
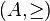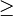("mayor o igual que") es antisimétrica, al igual que 
("mayor estricto que"), pues en este último caso, el antecedente de la definición nunca se cumple.
- Sea
, 
("menor o igual que") es antisimétrica, al igual que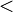 
("menor estricto que"), pues en este último caso, el antecedente de la definición nunca se cumple.
- La relación "ser más alto que" es antisimétrica, pues el hecho que a sea más alto que b y b sea al mismo tiempo más alto que a, es imposible.
La aplicación de cualquier relación R sobre un conjunto A, se representa con el par ordenado (A,R).
La definición de Antisimetría se apoya sobre la existencia previa de una Relación de Equivalencia RE.
La definición de Antisimetría se apoya sobre la existencia previa de una Relación de Equivalencia RE.
La definición de la Relación Antisimétrica significa que no coexisten en la relación pares simétricos
salvo los (x x) que están en la diagonal principal.
Esto se observa fácilmente tomando la Proposición Contrarrecíproca (PCR) de la definición dada:
PCR Proposición Contrarrecíproca
Las relaciones Antisimétricas son independientes y compatibles con las relaciones Simétricas y ASimétricas,
es decir las pueden ser simultáneas, como lo prueban los siguientes ejemplos:
A AxA A AxA
P. ejem. La relación ”madre de” es antisimétrica porque six es madre dey,
excluye ay es madre dex.
•En el grafo de unarelación
antisimétrica, ningún arco tiene un
compañero en dirección opuesta .
Equipo 5
Francisco Antonio Alberto
Gallardo Gaspar Saúl
Hernandez Gonzales Carlos
Hernandez Gonzales Carlos
Reyes Vite Ana Karen
Rodriguez Jalife Yael
RELACiON ANTISIMETRICA
ResponderEliminarLa relacion R sobre el conjunto A es antisim
etrica si para todos x; y 2 A se cumple que
si (x; y) 2 R y (y; x) 2 R ) x = y:
Una relacion es antisimetrica si y solo si M \
Mt In:
Existen en 2n:3
12
(n2n) funciones antisimetricas A.
buen trabajo compañeros somos equipo 6
La antisimetría no es lo opuesto de la simetría.
ResponderEliminarExisten relaciones que son simétricas y antisimétricas al mismo tiempo (como la igualdad), otras que no son simétricas ni antisimétricas (como la divisibilidad para los enteros), otras que son simétricas pero no antisimétricas (como la relación de congruencia módulo n), y otras que son antisimétricas pero no simétricas (como la relación "menor que").
Martinez de la Cruz Rodolfo,Hernandez Gabriel
Equipo 2.
(Juan Carlos,Norberto Cruz Gabriela,Gonsalez Teran Edith Monserrat.)
MARIZELA DE LA CRUZ dijo....
ResponderEliminarRELACION ANTISIMETRICA
_ La relación R sobre el conjunto A es antisimétrica si para todos x, y є A se cumple que si (x, y) є R y (y, x) є R x = y.
_ Una relación es antisimétrica si y solo si M Mt ≤ In.
_ Existen en 2n.31/2(n2-n) funciones antisimétricas A.
el trabajo me parecio interesante bien echo chavoxx
se dice que la relacion es antisimétrica cuando se da dos elementos de A que se relacionan entre sí mediante R, entonces estos elementos son iguales
ResponderEliminarRELACION ANTISIMETRICA:
ResponderEliminarUna relación binaria se dice que es antisimétrica si los pares ordenado (a,b) y (b,a) pertenecen a la relación entonces a = b:
Dicho de otra manera, no existen los elementos a, b distintos, y que a este relacionado con b y b este relacionado con a.
***BIEN EQUIPO***
***"" SOMOS EL EQUIPO 1 ***""
Equipo 7
ResponderEliminarbueno una Relacion antisimetrica son compatibles con las relaciones simetricas y asimetricas ya que (a) deveser simetrico a (b) para que pueda ser antisimetrico pero (b) no deve de ser simetrico a (b).
ya que de ser asi no secumpliria la regal de la antisimetria ya que es uno de los puntos mas importantes para que sean antisimetricos es decir a=b pero B no puede ser = a B.
y a y b deven sercompatibles en algum puto para ser simetrico porque de no ser asi no sepodria aser la antisimetria
int:
Gonzalo Garcez Cruz
Gonzales HErnandes Francisco Agustin
Anastacion Morales Janeth
Macario Cervantes Fernand